在计算机科学中，二叉树是一种常见的数据结构，广泛应用于各种算法和程序设计中，二叉树模型公式则是描述二叉树性质的重要工具，有助于我们更深入地理解二叉树的特性和操作，本文将详细介绍二叉树模型公式及其应用。

二叉树的基本概念

二叉树是一种树形结构，每个节点最多有两个子节点，通常称为左子节点和右子节点，在二叉树中，根节点是没有父节点的节点，其余节点或者是叶子节点（没有子节点），或者是内部节点（有两个子节点）。

二叉树模型公式

二叉树模型公式用于描述二叉树的性质，主要包括以下几个公式：

1、二叉树的节点数公式：对于任何非空二叉树，若其叶子节点数为n0，内部节点数为n1，总节点数为n（即n=n0+n1），则有公式：n=n0+n1+1，根节点数为1，因此总节点数等于叶子节点数与内部节点数之和加1，这个公式有助于我们快速计算二叉树的节点数量。

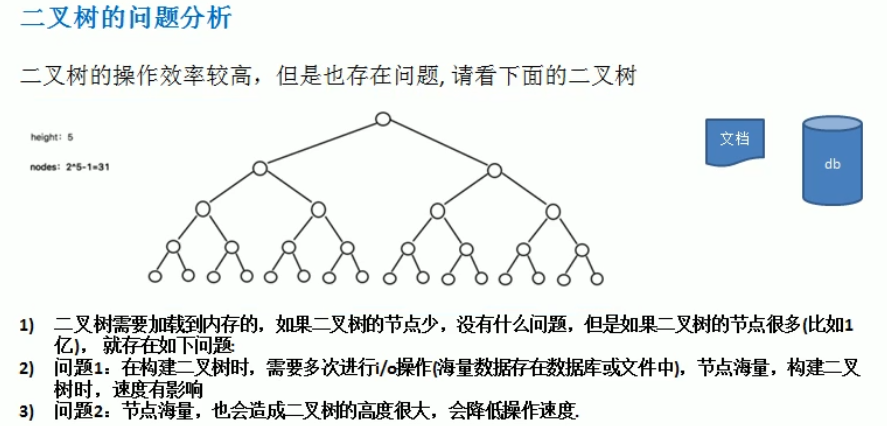
2、二叉树的深度公式：对于任何非空二叉树，其深度（或高度）h满足公式：h=log2N+1，其中N为节点的总数，这个公式可以帮助我们估算二叉树的深度，从而优化算法的时间复杂度。

3、二叉搜索树的性质公式：在二叉搜索树中，任意节点的左子树上的所有节点的值均小于该节点值，右子树上的所有节点的值均大于该节点值，这一性质使得二叉搜索树在查找、插入和删除操作中具有很高的效率。

二叉树模型公式的应用

二叉树模型公式在实际应用中具有广泛的应用场景，主要包括以下几个方面：

1、数据压缩：在数据压缩算法中，二叉树模型被广泛应用于构建Huffman编码树，通过构建Huffman编码树，可以实现数据的有效压缩和解压缩，二叉树模型公式的应用有助于我们理解Huffman编码树的构建过程和压缩效率。

2、排序算法：二叉搜索树在排序算法中具有重要的应用，通过构建平衡的二叉搜索树（如AVL树、红黑树等），可以在对数时间内完成查找、插入和删除操作，提高排序算法的效率，二叉搜索树的性质公式有助于我们理解这一过程的实现原理。

3、机器学习：在机器学习中，决策树是一种常用的模型，决策树的构建过程可以看作是一个二叉树的构建过程，二叉树模型公式有助于我们理解决策树的构建过程和性能评估。

4、图形界面设计：在计算机图形界面中，二叉树结构常用于描述界面元素的层次关系，通过应用二叉树模型公式，可以优化界面元素的布局和性能。

二叉树模型公式是描述二叉树性质的重要工具，有助于我们更深入地理解二叉树的特性和操作，本文介绍了二叉树的基本概念、模型公式以及在实际应用中的应用场景，通过学习和掌握二叉树模型公式，我们可以更好地应用二叉树数据结构解决实际问题，提高算法和程序的效率。